Meteorological Mast
Problem Statement
Design a meteorological mast that can withstand category 5 typhoons with tip deflection less than 0.5m, given the restrictions based on student number.
Given Values and Assumptions
The meteorological mast to be designed is 24 meters tall. Since my student number ends on an odd number, it must be a monopole. It must also be designed such that it can withstand a category 5 typhoon in the Philippines. According to the website of the Philippine Atmospheric, Geophysical and Astronomical Services Administration (PAGASA), the Public Storm Warning System classifies typhoons with sustained wind speeds of more than 220 kph as category 5 typhoons. For reference, the Joint Typhoon Warning Center (JTWC) has estimated that Typhoon Yolanda sustained wind speeds of up to 315 kph (Athawes, 2018). Yolanda was the most destructive typhoon to hit the country in recent years, so this sustained wind speed will be used as reference. Based on my student number, the meteorological mast will be placed in a low grass, open farmland terrain. This terrain will be a factor in determining the wind velocity’s effect on the mast.
Wind Profile
To create a wind force velocity profile seen by the mast, the wind speeds at varying elevations from 0 to 24 meters must first be determined. This can be done by applying the wind profile power law:
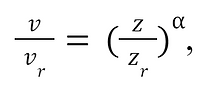
where v is the wind speed at elevation z, v is a known wind velocity at reference elevation z , and α is the power law wind shear exponent. This exponent is dependent on the roughness of the terrain. In their study, Delgado et al (2016) used the following table of values for some types of terrain and their corresponding wind shear exponent:
r
r
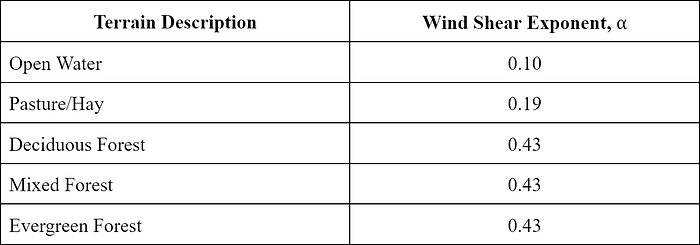
The terrain type in this table that most closely resembles the terrain assigned to me (low grass, open farmland) is pasture/hay. Thus, the wind shear exponent to be used is α = 0.19.
The known wind velocity can be set as 315 kph or 87.5 m/s, as discussed earlier, and the reference height is assumed to be 10 meters; according to Cumulus Wiki (n.d.), it is widely accepted that wind speed measurements are based on readings at an elevation of 10 meters above the ground. Given these values, the logarithmic wind profile seen by the mast can be characterized by the function
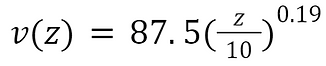
Since the main requirement of the meteorological mast is to not exceed a tip deflection of 0.5 m, the wind speed at the tip must be considered.
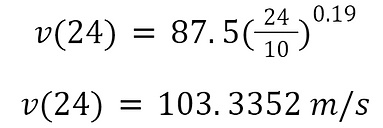
This function for wind speed can then be converted to a function of the wind’s dynamic pressure. The dynamic pressure can be considered as a fluid’s kinetic energy per unit volume. It can be defined by:
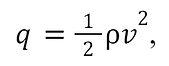
where ρ is the fluid’s density and v is its speed. Plugging in the density of dry air at STP (T=20℃, P=101.325 kPa) and the determined wind speed at the tip, we get the dynamic pressure experienced by the tower’s tip.

Pole Geometry
Before the force of the wind acting on the pole can be determined, the geometry of the tower must be decided on. There seems to be two common types of monopoles: telescopic and stepped. For this design project, I will be using the Single User 5G Monopole (SM2) of FLI Structures as a reference for the pole’s shape. This model of monopole tower has a tapered, telescopic structure with a top diameter of 400 mm or 0.4 m. According to FLI Structures’ tower selection guide, this model’s bottom diameter varies according to the requirements, so this parameter is estimated to be 0.6 m for now. Since the tower uniformly tapers, the diameter at any given elevation on the tower can be found with the equation
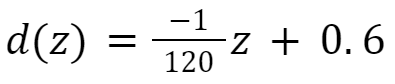
Jiangsu Hongguang Steel Pole Co., Ltd. sells steel for construction of monopoles. Based on their Alibaba page, they manufacture poles with wall thickness in the range of 2 to 30 mm; I chose to use a wall thickness of 15 mm or 0.015 m. They also offer several types of steel, but I chose hot rolled steel Q460, which has a Young’s modulus of 199.44 GPa and density of 7850 kg/m3 (American Society for Testing and Materials International, 2009).
Drag Force
Now, the drag force seen by the top of the mast due to the wind can be computed:
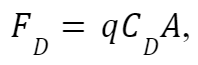
where C is the drag coefficient depending on the pole’s Reynold’s number and A is the area of the tower’s side profile seen by the wind. For this case, we assume that the entire length of the tower experiences the wind velocity at its maximum speed. Since the pole is uniformly tapered, this area can be seen as a trapezoid. Thus, the area as seen from its side is:
D

The drag coefficient now needs to be determined by solving for the Reynolds number. The problem with this tapered design is that since the Reynolds number is based on the shape’s diameter, there are different values for Reynolds number along the tower. To circumvent this, the average diameter throughout the tower is taken into consideration for calculating the Reynolds number. Kinematic viscosity of air at STP (T=20℃,P=101.325 kPa) is 15.06E-6 m2/s (Engineering ToolBox, n.d.).
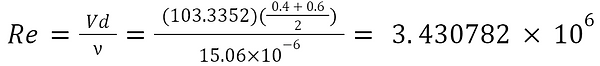
Inputting this Reynolds number in a drag coefficient calculator made by Dusling (n.d.), we get a drag coefficient of

Given all of these values, the drag force experienced by the top of the tower due to the maximum wind speed can be calculated

Tip Deflection
Based on a study conducted by Balagopal, Prasad Rao, and Rokade (2018), the lateral deflection caused by a lateral load at any point in a tapered steel pole can be characterized as:
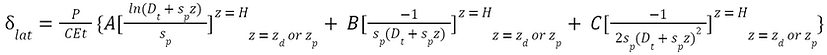
where P is the lateral load, E is the Young’s modulus, t is the thickness, D is the pole’s diameter at the tip, H is the pole’s height, z is the distance of the point of deflection from the top, and z is the distance of the applied point load from the top. Since the drag force due to the wind acts at the tip and the deflection requirement is also located at the tip, the values of z and z are 0. The slope of the pole s can be computed as:
t
d
p
d
p
p
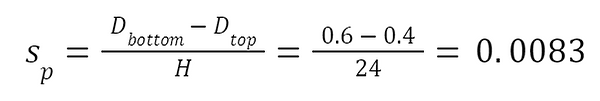
Constants A, B, and C can be computed with the following formulas:
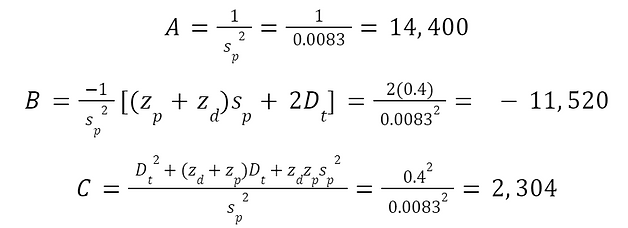
Plugging these values in to the equation for lateral deflection above,
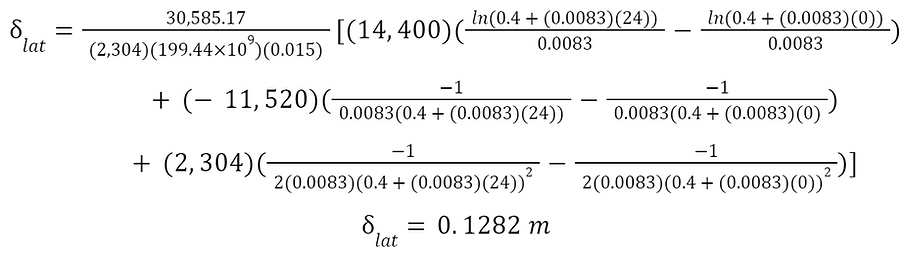
Materials
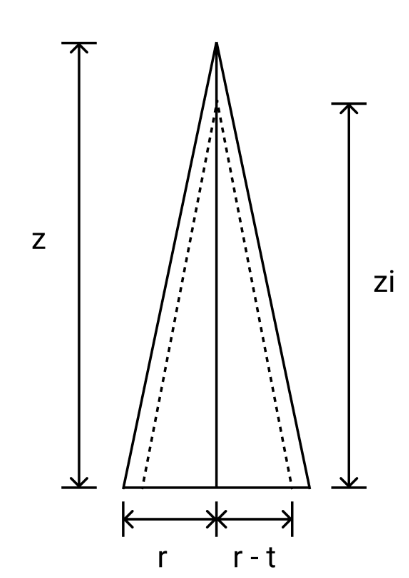
To determine the amount of materials to be used for this design, the total weight needs to be calculated. We must first “complete “ the tapered tower such that it is a hollow cone. The height of this “completed” tower can be determined by finding the point at which the diameter is 0.
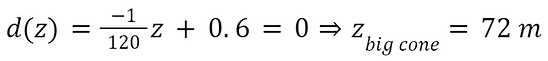
The height of the “inner cone” is also a necessary parameter to be determined. By similar triangles,
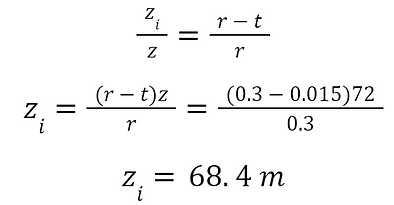
The volume of the tapered tower can be solved by determining the difference between the volumes of the cones.
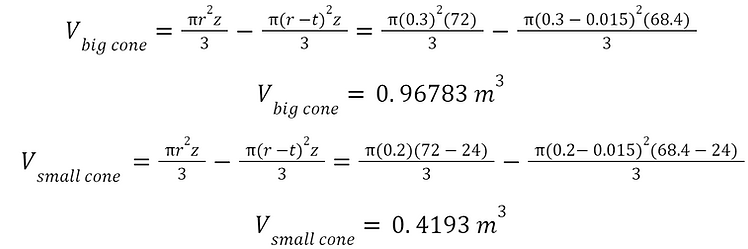
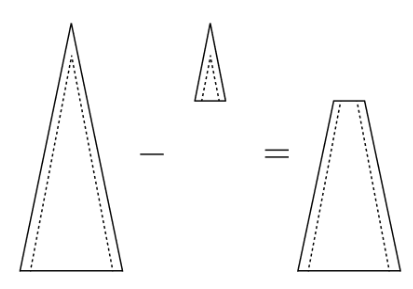
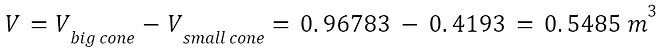
Using this volume and the density for Q460 steel, the total weight of materials can be determined.

From the Alibaba page of the previously mentioned company, they can sell their materials at a price of Php 50,283.80 per metric ton. This means that the total cost of materials would be around Php 226,277.10.
Conclusion
The meteorological mast is required to withstand a category 5 typhoon in the Philippines, with the tip deflecting less than half of a meter. It will be located in an area of open farmland, thus dictating the wind profile acting on it. The mast will have a tapered design, with a height of 24 m, top diameter of 0.4 m, base diameter of 0.6 m, and wall thickness of 0.015 m. The material to be used is hot rolled steel Q460. In a category 5 typhoon, the wind speeds will only cause a 0.1282 m deflection at the tip of the mast. The total cost of the materials amounts to Php 226,277.10.