Cantilevered Beam
Problem Statement
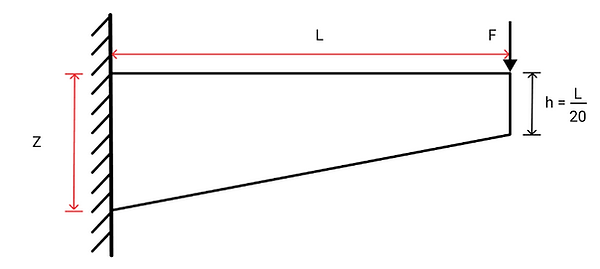
Design a tapered beam made out of AISI 304 stainless steel sheet, with length L and free end depth h such that when a force F is applied at the free end, there is a tip deflection of 1/40th of the beam length.
Given Values and Assumptions
A point load F is applied at the free end of a tapered cantilever beam, with length L. The free tapered end has a height of L/20. From my student number (2017-01093), L = 2.017m and F = 1.093kg, but since F is too small, 10kg is added for a total load of F = 11.093kg, which has an equivalent force solved by multiplying it by gravity F = (11.093)(9.81) kN. Due to this point load, the free end must have a deflection of Δ = L/40. The tapered beam is made out of AISI 304 stainless steel sheet. From this, the beam has a Young’s modulus of E = 193 GPa = 1.93E11Pa and density of ρ = 8000kg/m3.
Design Choices
Since the beam’s cross section is free choice, I decided on an I-section because based on my learnings from previous professors, an I shape cross section is ideal for beams to sustain forces. The moment of inertia and area of an I-section are given as:
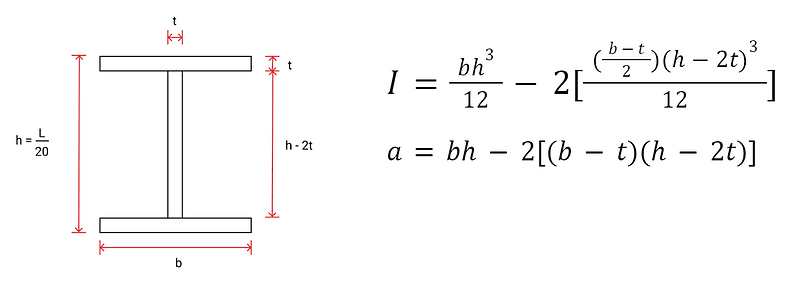
Another free design choice is the gauge of the stainless steel sheet, which determines the thickness of the sheet. For this design problem, I decided to use the thinnest possible sheet thickness. This is to prevent the load of the material’s weight from being heavier than the applied force. The sheet metal thickness that I decided on for this problem is t = 0.178mm or 36 gauge AISI 304 stainless steel sheet.
Determining Beam Width
Since a beam width value is not given, I decided to first assume that the beam has no taper, in order to get a general idea for a possible beam width value.

In this case, b is being solved for, thus I and a are functions of b. The weight of the beam is first solved for because it contributes to the moment at the fixed end. The distributed load due to the weight of the beam can be solved as
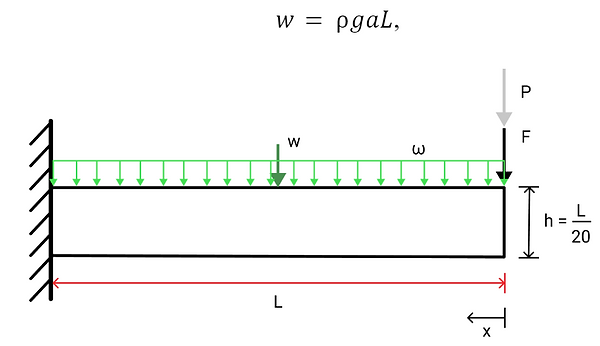
Given this, Castigliano’s theorem is applied. According to Castigliano’s theorem, the deflection at the free end is given as the partial derivative of the total elastic strain energy with respect to the point load.

A fictitious load P is applied at the free end in order to apply Castigliano’s theorem. A moment function is then formed, based on the fixed end to cancel out the reaction forces.

Finding the partial derivative of this function in terms of P,

Since P is a fictitious load, its actual value is P = 0.
Instead of using the exact desired value for deflection, I chose to use a value that is greater: δ = L/39. This way, when the resulting width value is used in the case where the beam is tapered, there is more guarantee that the solved height at the fixed end is greater than the height at the free end.
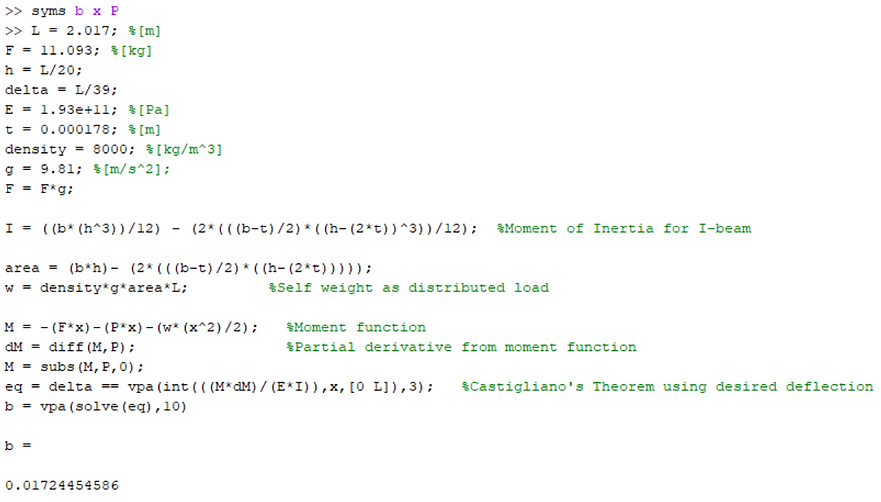
Now, known values can be substituted into the equation from Castigliano’s theorem.
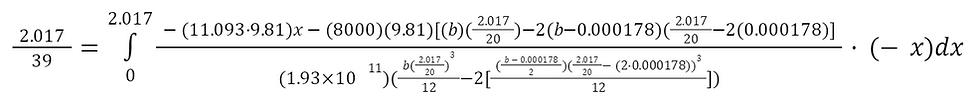
Solving for b, we get a value of
Checking for Negligibility of Beam Weight
Using the solved beam width, we find that the resulting point load due to the weight of the beam is
which is less than 5% of the total load w + F.

This means that the beam’s self weight can be disregarded. Castigliano’s theorem can be applied again, but omitting the beam’s self weight in the moment function.
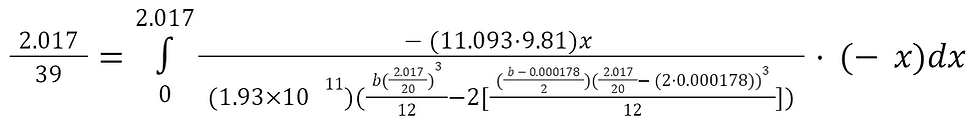
Solving for b once again, we get a working beam width of

Determining Height at Fixed End
Now that an approximate beam width is identified, we can focus on the case where the beam is tapered. Before finding the total area of sheet metal needed, the height at the fixed end of the tapered beam must be determined. The concept of similar triangles can be applied here by extending the top and bottom of the beam, such that there is some distance d from the free end of the beam to the tip of the imaginary triangle.
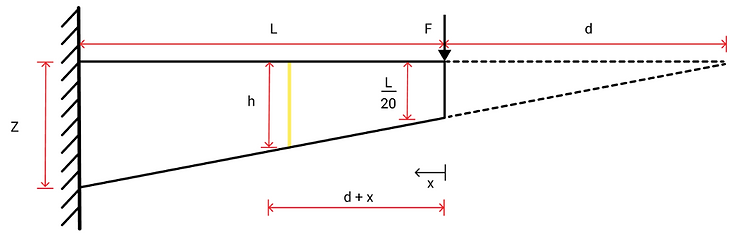
The height of the beam varies in this case; this calls for the statement of height h as a function of length x along the beam. From similar triangles, we see that
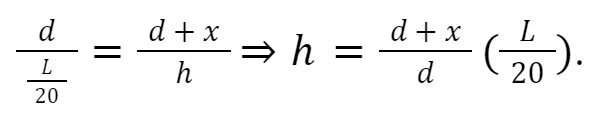
For this portion, the same given values are used except the moment function M is now a function of x. In using Castigliano’s theorem for this part, the value used for the deflection is the actual desired deflection. Once again, the weight of the beam is omitted in the moment function because it is negligible compared to the applied load.

Solving for distance d, we get a value of
From similar triangles again, we see see that height at fixed end Z can be expressed as
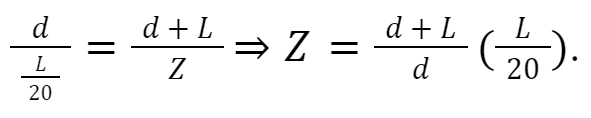
Substituting d = 149 into this expression,

Materials for Constructing Beam
The total weight of the beam can be computed for by summing the weights of each component. In the case of a tapered beam with an I-section, the beam can be divided into its three parts: straight top flange, trapezoidal web, and angled bottom flange. The volumes of each part can be calculated with the following respective expressions:

Taking the summation of these volumes and multiplying it by the density of the material will yield the total weight of the material used for the beam.


Beam Manufacturing Process
The material to be used to manufacture the beam is sold in sheets, so an ideal cutting process for this situation would be shearing, especially since the cuts would all be straight cuts. Specifically, a foot-operated shear would work well because the work pieces would not be too big. In joining the components of the beam, I initially decided to use cold welding. Cold welding can be used in joining thin sheets of metal because there is no heating or fusion involved in the process. However, I consulted with a welding specialist from Toolec Inc. and he informed me that TIG welding might be the better option due to complexity in cold welding. During my inquiry with a representative from Korweld Inc., they mentioned that it might be very difficult to weld the materials together due to the very thin specs, but might be doable with their company’s 1.6mm stainless steel welding filler rod. According to the representative, 1kg of this filler rod would cost about PHP200.
On another call with a sales representative from Sanyo Seiki Stainless Steel Corp., I was informed that the thinnest AISI 304 stainless steel sheet that they sell is 24 gauge, at PHP280 per 4”x8” sheet. Assuming the company could manufacture custom sheets that fit my specifications, their price for stainless steel sheet per kilogram could be expressed as
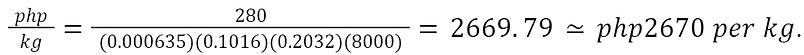
Applying this to the required amount of material,
